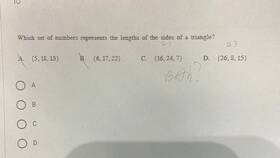В математических задачах часто встречаются условия, где известны сумма и произведение некоторых величин. Рассмотрим основные методы работы с такими данными.
Содержание
В математических задачах часто встречаются условия, где известны сумма и произведение некоторых величин. Рассмотрим основные методы работы с такими данными.
1. Основные понятия и формулы
| Понятие | Обозначение | Формула |
| Сумма двух чисел | S = x + y | Основное соотношение |
| Произведение двух чисел | P = x × y | Основное соотношение |
| Теорема Виета | - | x² - Sx + P = 0 |
2. Типовые задачи и методы их решения
2.1. Нахождение чисел по известным сумме и произведению
- Составляем квадратное уравнение: t² - St + P = 0
- Находим дискриминант: D = S² - 4P
- Вычисляем корни: t = [S ± √D]/2
- Получаем искомые числа
2.2. Пример решения
Дано: S = 5, P = 6. Найти числа.
- Составляем уравнение: t² - 5t + 6 = 0
- D = 25 - 24 = 1
- t₁ = (5 + 1)/2 = 3
- t₂ = (5 - 1)/2 = 2
- Ответ: 2 и 3
3. Применение в различных разделах математики
| Раздел | Применение |
| Алгебра | Решение квадратных уравнений |
| Геометрия | Нахождение сторон прямоугольника |
| Тригонометрия | Преобразование выражений |
| Математический анализ | Исследование функций |
4. Полезные следствия
- Сумма квадратов: x² + y² = S² - 2P
- Сумма кубов: x³ + y³ = S³ - 3SP
- Сумма обратных величин: 1/x + 1/y = S/P
- Разность чисел: x - y = √(S² - 4P)
Важное замечание
Для существования действительных чисел по заданным S и P необходимо выполнение условия: S² ≥ 4P. Это следует из требования неотрицательности дискриминанта.
