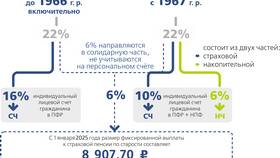
Сумма сторон треугольника, также известная как периметр треугольника, представляет собой одну из основных характеристик этой геометрической фигуры. Периметр вычисляется как сумма длин всех трех сторон треугольника.
Содержание
Сумма сторон треугольника, также известная как периметр треугольника, представляет собой одну из основных характеристик этой геометрической фигуры. Периметр вычисляется как сумма длин всех трех сторон треугольника.
Формула расчета периметра треугольника
Для любого треугольника со сторонами a, b и c периметр (P) вычисляется по формуле:
P = a + b + c
Особенности расчета для разных типов треугольников
| Тип треугольника | Особенности расчета |
| Равносторонний | P = 3 × a (все стороны равны) |
| Равнобедренный | P = 2 × a + b (две стороны равны) |
| Разносторонний | P = a + b + c (все стороны разные) |
| Прямоугольный | Можно использовать теорему Пифагора для нахождения неизвестной стороны |
Примеры расчета
Пример 1: Равносторонний треугольник
Для треугольника со стороной 5 см:
P = 3 × 5 = 15 см
Пример 2: Разносторонний треугольник
Для треугольника со сторонами 3 см, 4 см и 5 см:
P = 3 + 4 + 5 = 12 см
Практическое применение
Знание суммы сторон треугольника применяется в различных областях:
- В строительстве для расчета материалов
- В ландшафтном дизайне
- В производстве треугольных деталей
- В навигации и геодезии
Связь периметра с другими параметрами треугольника
Периметр треугольника связан с другими его характеристиками:
- Используется в формуле Герона для вычисления площади
- Связан с радиусами вписанной и описанной окружностей
- Играет роль при решении задач на подобие треугольников
Важные свойства
- Для любого треугольника сумма двух сторон всегда больше третьей стороны
- Периметр всегда положительная величина
- Изменение одной стороны влияет на общий периметр
Понимание принципов расчета суммы сторон треугольника является фундаментальным знанием в геометрии и находит применение во многих практических задачах.
